La mayoría de las personas confían en los resultados que les entregan en un examen de sangre. Sin embargo, muchas desconfían de los resultados de una encuesta. ¿Por qué? Ambos son “estudios”, y ambos utilizan muestras para obtener sus conclusiones.
El sentido común nos puede jugar una mala pasada. Para un examen médico es natural pensar que solo tomando una parte podremos saber el estado de todo el cuerpo. Pero al parecer, no resulta natural pensar que las encuestas, pese a que también entrevistan solo un grupo de personas, representen a toda la población.
Pero la verdad es que hacer una buena muestra para una encuesta tiene mucho de ciencia, y puede ser entendido parecido a ese examen de sangre.

Para enfrentar esta desconfianza, veremos críticas o dudas respecto a encuestas que comúnmente encontramos en redes sociales. Aquí trataremos de responder algunas de ellas:
¡2.000 personas son muy pocas para representar lo que piensan las personas en Chile!
2.000 casos para representar a aproximadamente 18 millones de personas en Chile realmente parece ser un número bajo… pero gracias a la estadística este número —dependiendo del fenómeno que queramos estudiar1— será suficiente.
De hecho, un reflejo del poder de una muestra —y para seguir con el mismo ejemplo— es que para detectar una determinada dolencia, no es necesario extraer ni toda, ni la mitad, ni siquiera un octavo de nuestra sangre. En promedio una persona contiene ~5 litros de sangre, pero solo bastan entre 10-12 ml (un 0.0024% del total) para conocer lo que sucede. Lo mismo ocurre con las encuestas… para saber qué opinan las personas sobre el gobierno de turno, no es necesario preguntarle a una gran proporción de la población en Chile.
Aquí les mostramos un pequeño ejemplo de la magia de la estadística. Primero, crearemos a toda nuestra población (de 1.000 personas en total), con una distribución muy similar entre hombres y mujeres (49% y 51%, respectivamente). Puedes ver a nuestra población en la figura 1!
poblacion <- data.frame(Sexo = c(rep('Hombre', 490), c(rep('Mujer', 510))))
poblacion %>%
count(Sexo) %>%
ggplot(aes(fill = Sexo, values = n)) +
geom_waffle(n_rows = 40, size = 0.5,
colour = "white",
radius = unit(3, "pt"),
nudge_x = -11) +
annotate('text', x = (25 * c(.25, .75)) + 0.5, y = c(20, 20), label = c("49%", "51%"),
colour = 'white',
size = rel(13), hjust = 0.5) +
scales_charts +
labs(title = 'Todas las personas ordenadas según sexo')
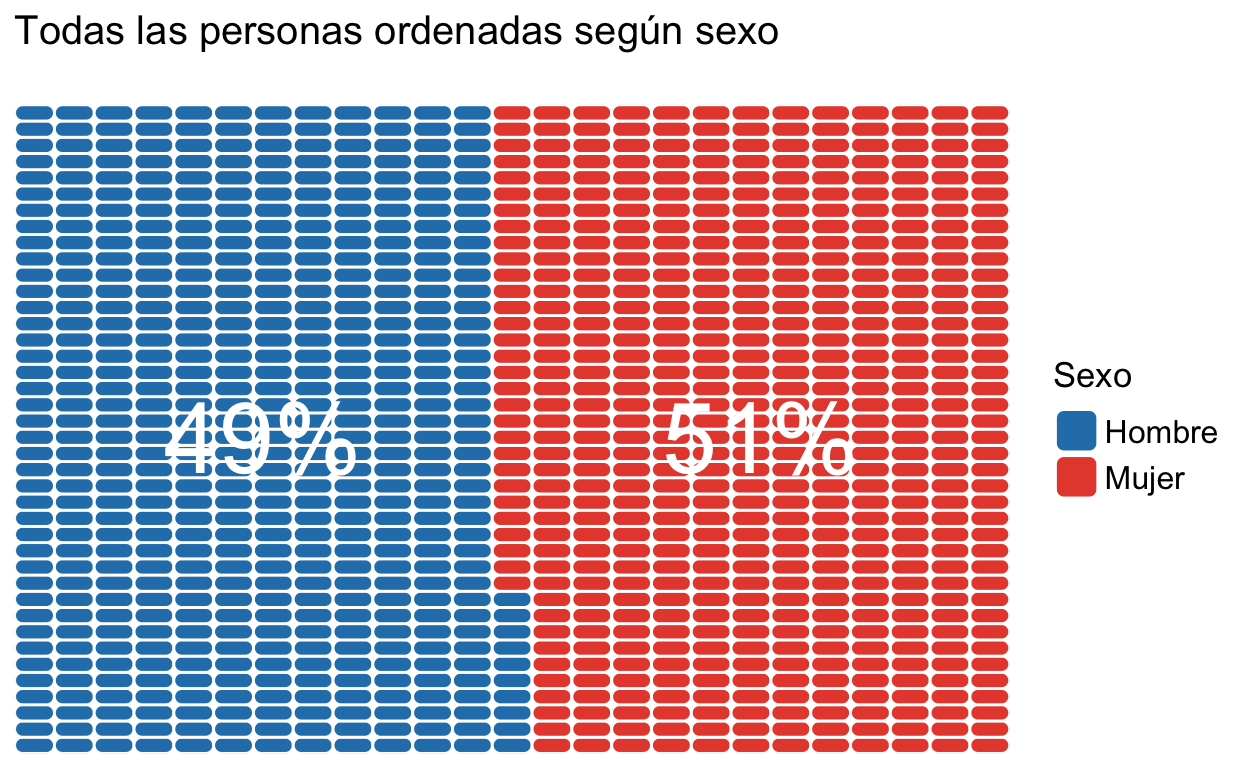
Figure 1: Población
Luego, tomamos una muestra de 100 personas al azar, y veremos la distribución de sexo en ella… ¡Es muy parecida a la población!2 ¿Magia? No, estadística.
set.seed(123)
muestra <- slice_sample(poblacion, n = 100, replace = TRUE)
muestra %>%
count(Sexo) %>%
ggplot(aes(fill = Sexo, values = n)) +
geom_waffle(n_rows = 10, size = 0.5,
colour = "white",
radius = unit(3, "pt")) +
annotate('text', x = (10 * c(.25, .75)) + 0.5, y = c(5.5, 5.5), label = c("50%", "50%"),
colour = 'white',
size = rel(13), hjust = 0.5) +
scales_charts +
labs(title = 'Distribución de sexo en muestra')
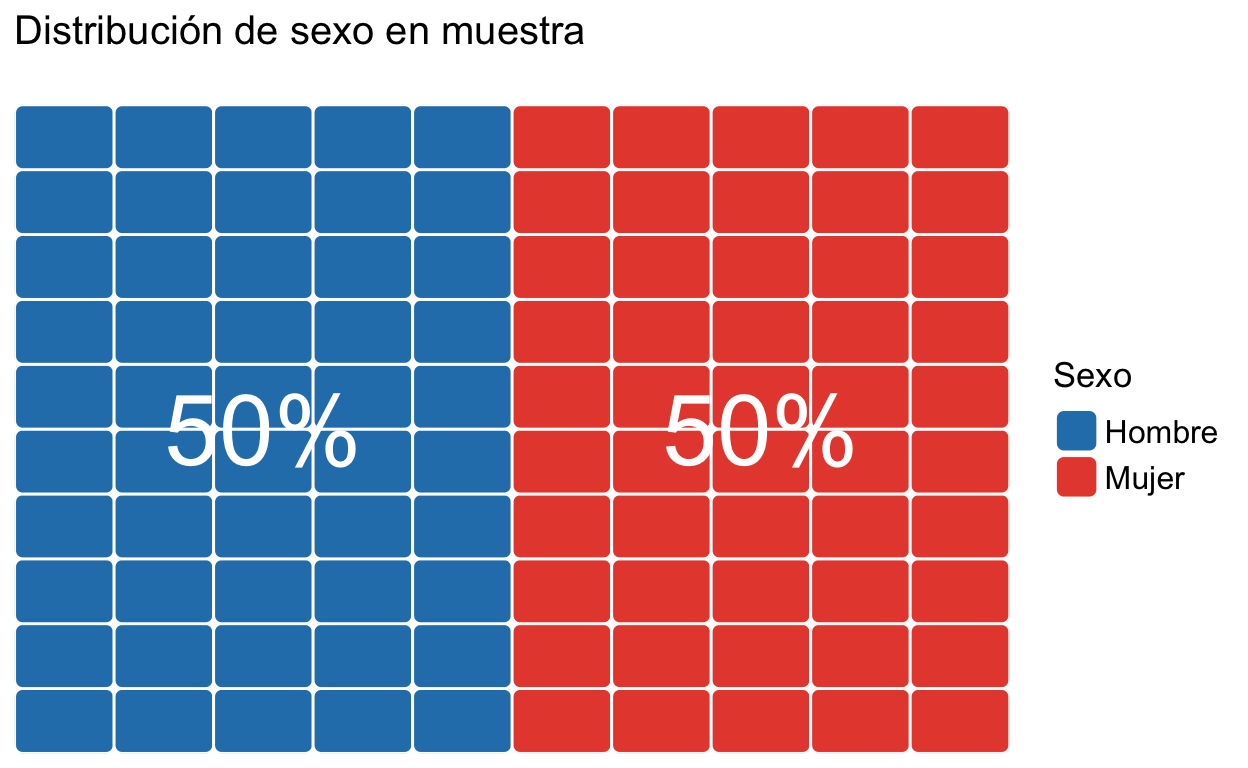
Figure 2: Muestra
Ahora bien, si queremos diagnosticar una rara enfermedad (en un caso médico) o estudiar un fenómeno peculiar en la sociedad, requerimos de un conjunto de exámenes específicos para lo primero, y muestras más grandes o sofisticadas para lo segundo.
¡A mi nunca me han encuestado… no creo en las encuestas!

Las encuestas tienen tamaños muestrales muy variados, y esto dependerá de los objetivos y fenómenos que quieran medir —como explicamos en el punto anterior—, pero también de limitaciones presupuestarias, del tiempo disponible para recolectar las respuestas, entre otros.
Para contextualizar, la encuesta Encuesta Nacional Urbana de Seguridad Ciudadana (ENUSC) —de las más grandes en Chile— puede llegar a tener un tamaño muestral cercano a las 25.000 entrevistas. De esta manera, y haciendo un simple cálculo de \(25.000/18.000.000 = 0.001\%\) vemos que las probabilidades de participar en una encuesta (¡incluso en las más grandes!) es muy baja.
De ahí que, muy probablemente, la gran mayoría de las personas nunca participará en una encuesta, e incluso no conocerá a nadie que lo haga.
Ahora, también es importante notar que existen encuestas sociales (como ENUSC, Casen, o las que realizamos en DESUC) y encuestas de consumo general. Probablemente, muchos de quienes leen esta entrada han sido parte de estas últimas sin considerarlas como “encuestas”. ¿Recuerdan haber sido llamados para que evalúen al ejecutivo de banco que los acaba de atender en una solicitud? ¡Eso también es una encuesta!
¿De dónde salieron las personas?
¿Cómo las escogieron?

Esta es una pregunta muy relevante, porque apunta directamente a la representatividad de la muestra. Para medir y entender la opinión de las personas, deseamos que nuestras muestras sean representativas, es decir, que sean similares a la población. Para ello debemos utilizar métodos específicos para seleccionar una buena muestra.
Y este es un punto que queremos dejar en claro: hay muestras buenas y muestras malas. Tal como en la medicina obtener una muestra de tejido de hígado probablemente no nos ayude a encontrar enfermedades pulmonares, una encuesta realizada únicamente a la salida en estaciones del metro, o solo llamando a teléfonos fijos, nos darán una visión parcial sobre lo que sucede.
Entonces… ¿cómo debe ser una buena muestra? Bueno, para eso tendrán que leer nuestra siguiente entrada.
Si nos interesa estudiar un fenómeno que solo afecta a un pequeño grupo de personas, por ejemplo, jugadores de tenis, será necesario preguntar a muchas personas qué deportes practican para lograr entrevistar a suficientes jugadores de tenis.↩︎
Sabemos que no es exactamente igual (49%-51% v/s 50%-50%), pero este margen de error es esperable —incluído en estudios médicos—, y podremos hablar específicamente sobre él en un próximo post.↩︎